آموزش زبان پایتون – ساختار داده ای مجموعه (set)
مقاله قبلی: دیکشنری و نحوه ایجاد آن در زبان برنامه نویسی پایتون
در این مقاله شما اطلاعاتی را در خصوص ساختار داده ای مجموعه ها (مجموعه ها) خواهید آموخت. اطلاعاتی از قبیل ایجاد مجموعه ها، اضافه کردن آیتم هایی به مجموعه ها، حذف آیتم های یک مجموعه و سایر عملیات مربوط به مجموعه ها.
نوع داده مجموعه و نحوه ایجاد آن
set ها به مجموعه ای از داده های نا مرتب و unindexed گفته می شود. درحقیقت همان طور که در ریاضیات آموختیم مجموعه به دسته ای از اشیاء متمایز با هم گفته می شود به طوری که ترتیب قرار گیری عناصر اهمیتی ندارد.

برخلاف خود مجموعه که تغییر پذیر است یعنی می توان عناصری را به آن اضافه نمود یا از آن حذف کرد، اعضای یک مجموعه منحصر به فرد هستند و نباید تغییر کنند. این نوع ساختار داده می تواند دارای هر تعداد داده ای باشند. علاوه بر این اعضای مجموعه می تواند از هر نوعی باشند (عدد صحیح، اعشاری، تاپل ، رشته و غیره). اما نمی توان از دیکشنری ها و لیست ها به عنوان اعضای پایتون استفاده کرد. چون این دو نوع داده تغییر پذیر هستند.
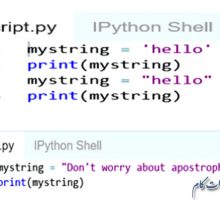
اعضای یک مجموعه در درون یک جفت براکت مجعد { } قرار گرفته و با علامت کاما از هم جدا می شوند. در مثال های زیر می توانید مجموعه هایی را ببینید که همه اعضای آن از نوع رشته، عدد و یا ترکیبی از عدد اعشاری و رشته و تاپل هستند.
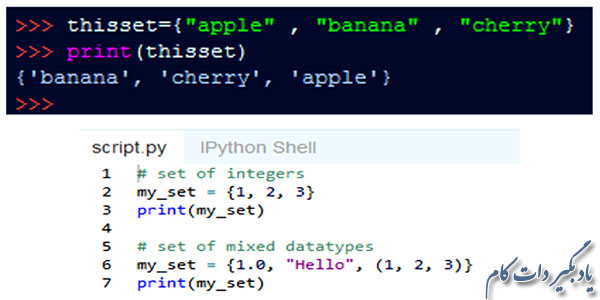
مجموعه ها نمی توانند دارای اعضای تکراری باشند و در صورت استفاده از مقادیر تکراری در آن ها، آیتم های تکراری حذف می شوند. مثلا در قطعه کد زیر می بینید که نسخه های تکراری داده ها به طور خودکار نادیده گرفته می شوند. هم چنین شما مجاز به قرار دادن لیست ها و دیکشنری ها در داخل مجموعه نیستید و در صورت عدم رعایت این موضوع، با خطای TypeError مواجه خواهید شد.
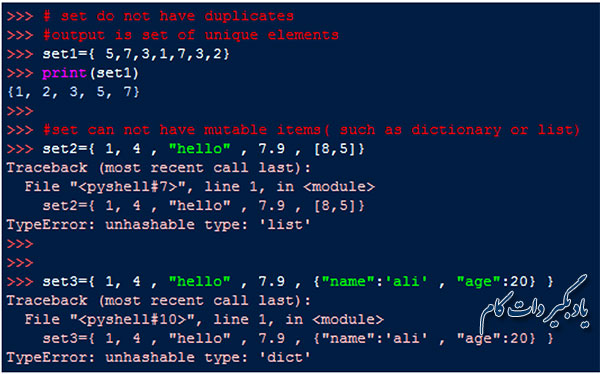
علاوه بر این شما می توانید با استفاده از تابع سازنده مجموعه، نیز مجموعه مورد نظر خود را ایجاد کنید. در این روش باید اعضای مجموعه را به جای براکت مجعد در داخل دو علامت پرانتز قرار دهید.

ایجاد یک مجموعه خالی
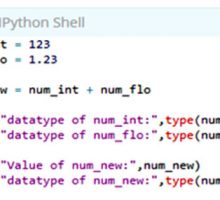
از آن جا که اعضای یک مجموعه در داخل براکت مجعد قرار می گیرند، شاید اگر از شما بپرسیم که یک مجموعه خالی را چگونه ایجاد می کنند بگویید که با یک جفت براکت مجعد {}. اما این طور نیست. چرا که یک جفت براکت مجعد در پایتون یک دیکشنری خالی ایجاد می کند نه مجموعه خالی. بنابراین برای این کار باید از تابع مجموعه بدون هیچ گونه آرگومانی استفاده کنید. برای اطمینان از این موضوع، می توانید همانند مثال زیر از تابع type استفاده کنید.
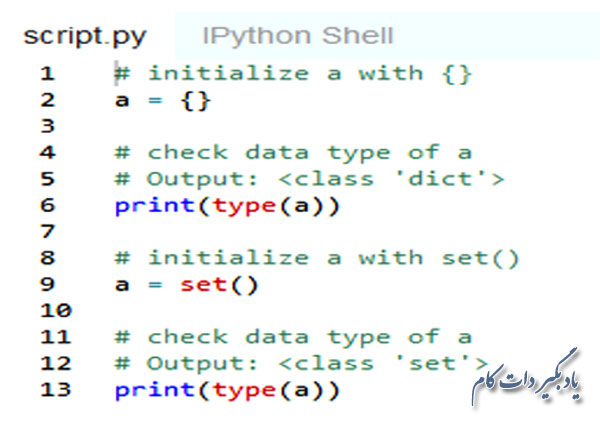
نحوه دسترسی به اعضای یک مجموعه
از آن جا که مجموعه ها، نوع داده نا مرتب هستند بنابراین نمی شود توسط اندیس به اعضای آن دسترسی پیدا کرد (دسترسی با اندیس، منجر به خطای TypeErrorمی شود) اما می توان توسط یک حلقه for تمامی اعضای یک مجموعه را پیمایش نمود و عملیات مورد نظر را روی آن ها انجام داد. همین طور مشابه لیست ها، دیکشنری ها، تاپل ها و رشته ها، می توانید با استفاده از عملگر و کلمه کلیدی in، حضور یا عدم حضور عنصری را در یک مجموعه مورد بررسی قرار دهید.
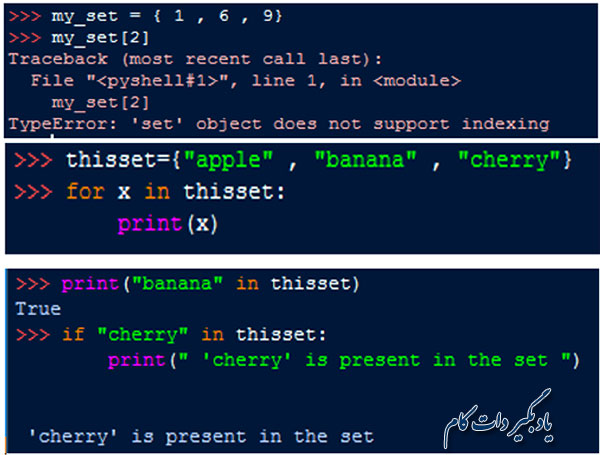
تغییر اعضای یک مجموعه
وقتی یک مجموعه ایجاد کردید دیگر نمی توانید اعضای آن را تغییر دهید با این حال، می توانید عناصر جدیدی به آن اضافه کنید.
نحوه اضافه کردن آیتم به یک مجموعه
اگر قصد اضافه کردن یک عنصر را دارید از تابع add() و در صورتی که می خواهید بیش از یک عنصر را اضافه کنید از تابع update() استفاده کنید.
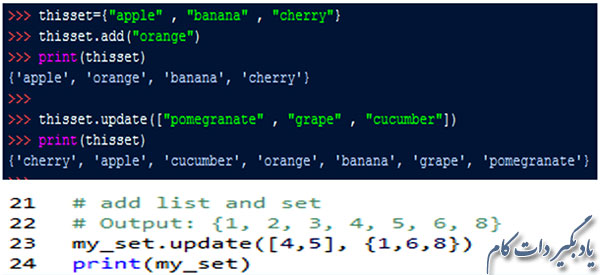
محاسبه طول مجموعه
برای اطلاع یافتن از تعداد اعضای یک مجموعه از تابع len() استفاده کنید.

حذف یک آیتم
برای حذف هر یک از اعضای مجموعه می توان از تابع remove() یا تابع discard() استفاده کرد. تنها تفاوت این دو تابع، این است که درصورتی که عنصر مورد نظر برای حذف یافت نشود، تابع remove() خطای KeyError بر می گرداند حال آن که تابع discard() در چنین شرایطی، هیچ خطایی را گزارش نمی کند.
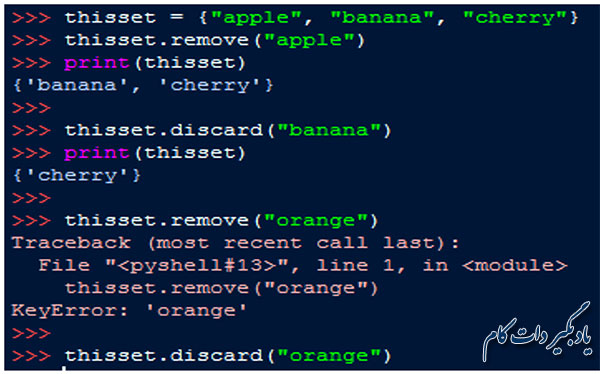
شما برای حذف یک عنصر، می توانید از تابع pop() نیز استفاده کنید مقدار برگشتی این تابع، عنصر حذف شده است. اما باید بدانید که این تابع در مجموعه ها برخلاف دیکشنری ها، آخرین عنصر را حذف می کند و از آن جایی که مجموعه ها، داده ها نا مرتب هستند لذا در صورت استفاده از این تابع، نمی توانید بفهمید که کدام عنصر حذف می شود. در حقیقت این تابع هر بار یک عنصر را به تصادف انتخاب کرده و حذف می کند.
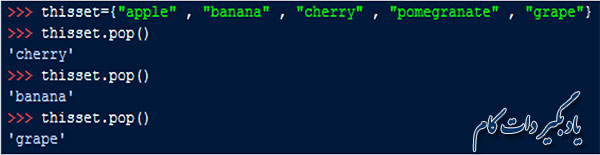
خالی کردن و حذف یک مجموعه
در این جا هم مشابه دیکشنری ها می توان برای حذف یک باره همه عناصر یک مجموعه از تابع clear() و برای حذف کامل یک مجموعه از کلمه کلیدی del استفاده کرد.
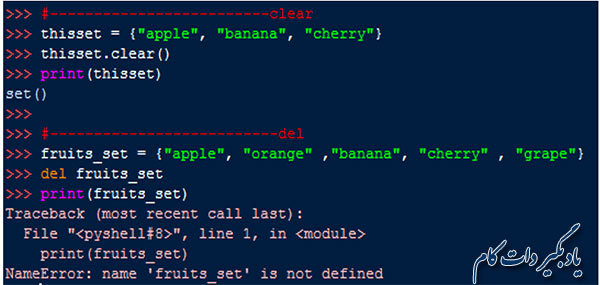
تبدیل ساختارهای داده ای دیگر به لیست
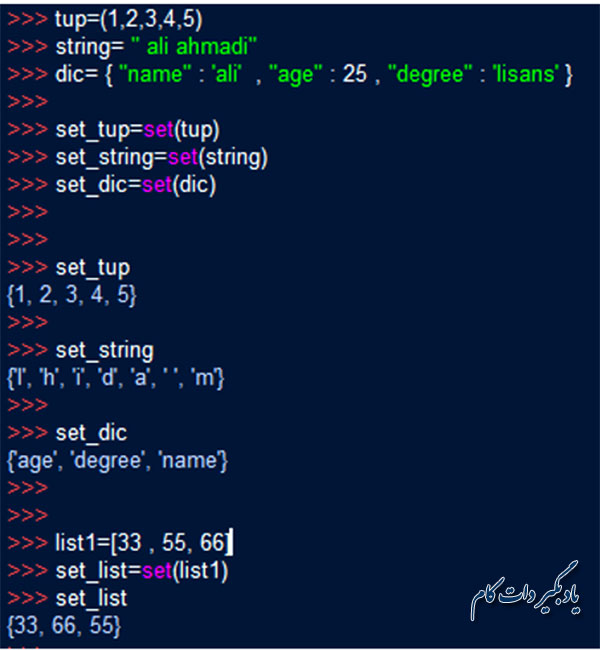
شما می توانید سایر ساختارهای داده ای نظیر رشته، لیست، تاپل و حتی دیکشنری را هم به مجموعه تبدیل کنید برای این کار کافیست که نام ساختار داده ای مورد نظرتان را به عنوان پارامتر به تابع set ارسال کنید. با دقت در مثال زیر می توانید چند نکته را متوجه شوید. مثلا ملاحظه می کنید که ایتم های اضافی رشته string، پس از تبدیل شدن به مجموعه کاراکتر، به صورت خودکار حذف شده اند. مضاف بر این که ترتیب کاراکترها هم در مجموعه حاصل، الزاما رعایت نشده است. یا می بینید که به هنگام تبدیل شدن دیکشنری dic، به یک مجموعه، مقادیر آن حذف شده و تنها کلیدها باقی مانده اند و این کلیدها هستند که آیتم های مجموعه را تشکیل می دهند.
ترکیب مجموعه ها با دیکشنری ها
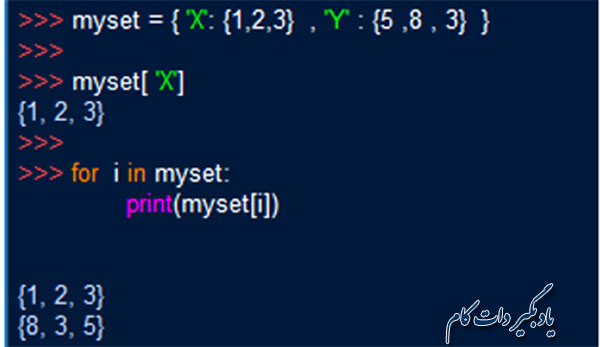
جالب است بدانید که شما می توانید مجموعه ها را با دیکشنری ها هم ترکیب کنید. در قطعه کد زیر نمونه ای از این نوع ترکیب و نحوه دسترسی به عناصر مجموعه را مشاهده می کنید.
به دست آوردن اجتماع، اشتراک و تفاضل دو مجموعه
همان طور که شما در ریاضیات پس از فراگیری اعداد، می توانستید توسط اعمال عملگرهای ریاضی بر روی آن ها، اعداد جدیدی را تولید کنید در پایتون هم می توانید با اعمال یک سری توابع یا عملگرها بر روی مجموعه ها، مجموعه های جدیدی ایجاد کنید.
بنابراین از مجموعه ها می توان برای انجام اعمال ریاضی مجموعه ها نظیر اجتماع، اشتراک و تفاضل نیز استفاده کرد.
فرض کنید که دو مجموعه A و B داریم و می خواهیم اجتماع آن ها را به دست بیاوریم.
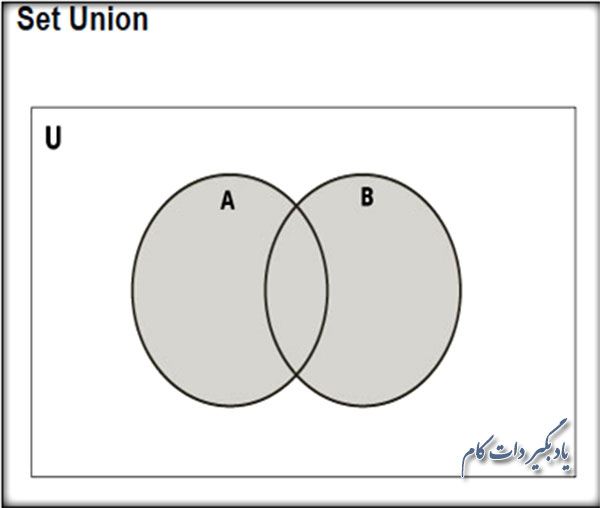
در قطعه کد زیر می توانید شیوه به دست آورد اجتماع دو مجموعه را توسط عملگر | یا تابع union ببینید. ملاحظه می کنید که اعضای اجتماع دو مجموعه A و B، آیتم هایی هستند که یا در A هستند یا در B یا در هر دو. به عبارت دیگر، اجتماع دو مجموعه، مجموعه ایست که تمامی اعضای آن دو مجموعه را دارد.

همان طور که در مثال بالا می بینید با این که عدد 5 در هر دو مجموعه A و B وجود دارد ولی تنها یک بار در اجتماع دو مجموعه ظاهر شده است در نتیجه یکی از مهم ترین ویژگی مجموعه ها، منحصر به فرد بودن اعضای آن است یعنی تکرار آیتم ها در آن تاثیری ندارد.

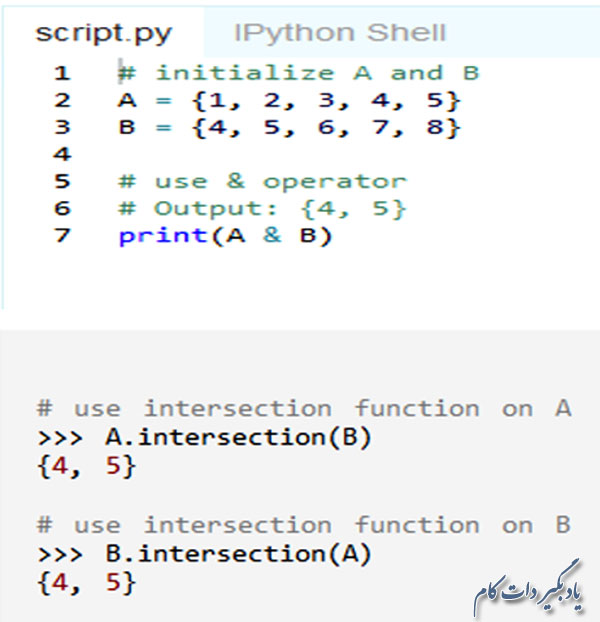
اشتراک دو مجموعه A و B هم مجموعه ایست که اعضای آن بین آن دو مجموعه مشترک باشند.
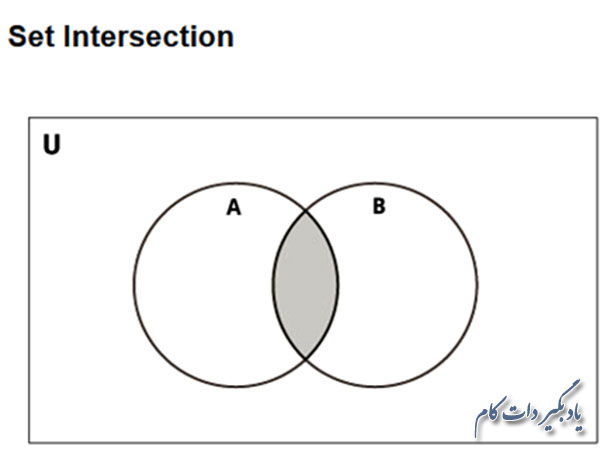
برای به دست آوردن اشتراک دو مجموعه هم می توانید از عملگر & یا تابع intersection() استفاده کنید.
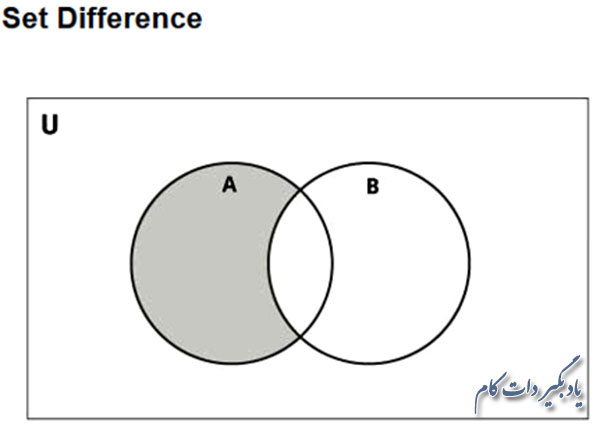
اختلاف دو تابع A و B نیز مجموعه ایست که آیتم هایی از اعضای مجموعه اول را بر می گرداند که در مجموعه دوم وجود ندارند. مثلا A-B اعضایی را بر می گرداند که تنها در مجموعه A هستند نه در مجموعه B. به طور مشابه B-A نیز اعضایی را بر می گرداند که تنها در مجموعه B هستند نه در مجموعه A.
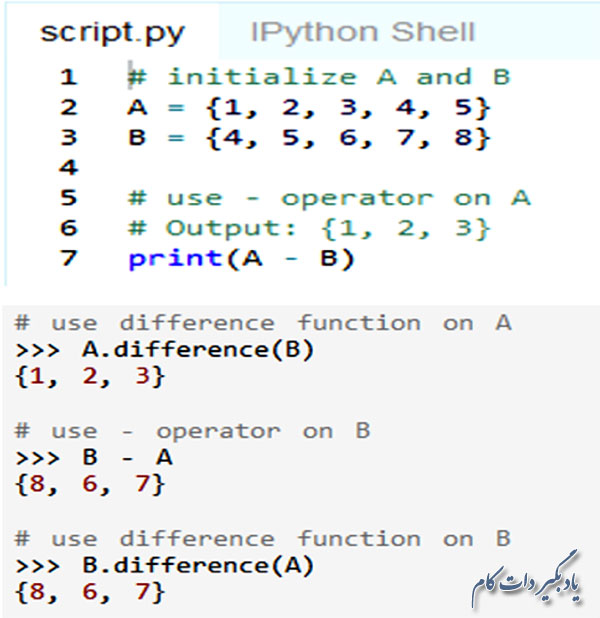
برای به دست آوردن اختلاف دو تابع هم می توان از عملگر منها (-) یا تابع difference() استفاده کرد.
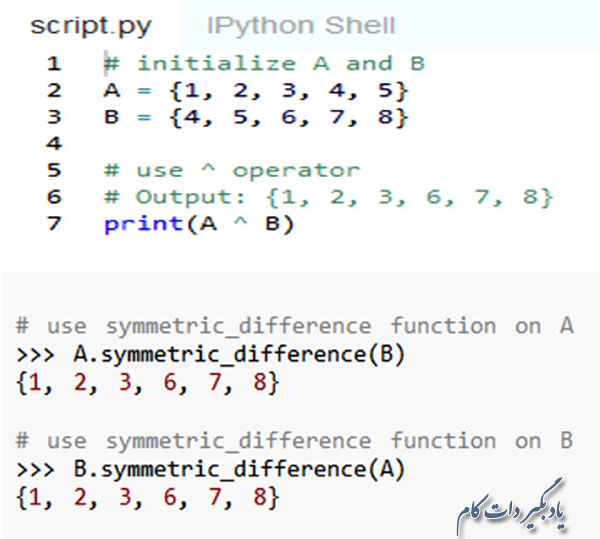
تفاضل متقارن A و B مجموعه ایست که تمامی اعضای دو مجموعه A و B را به جز اعضای مشترک این دو، دارا می باشد. به عبارت دیگر تفاضل متقارن A و B، اجتماع دو مجموعه A-B و B-A است.
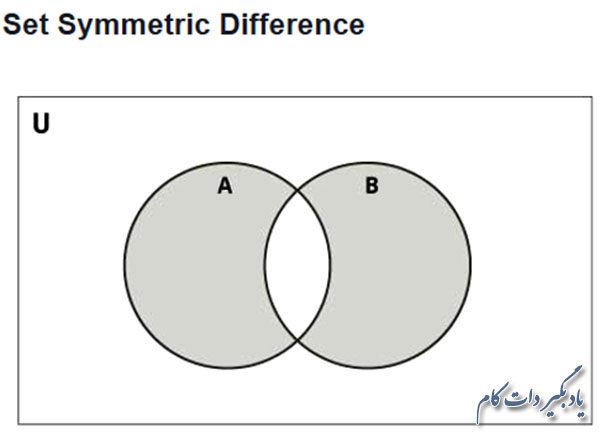
تفاضل متقارن مجموعه ها را می توانید توسط عملگر ^ یا تابع symmetric_difference() به دست بیاورید.
تابع isdisjoint()
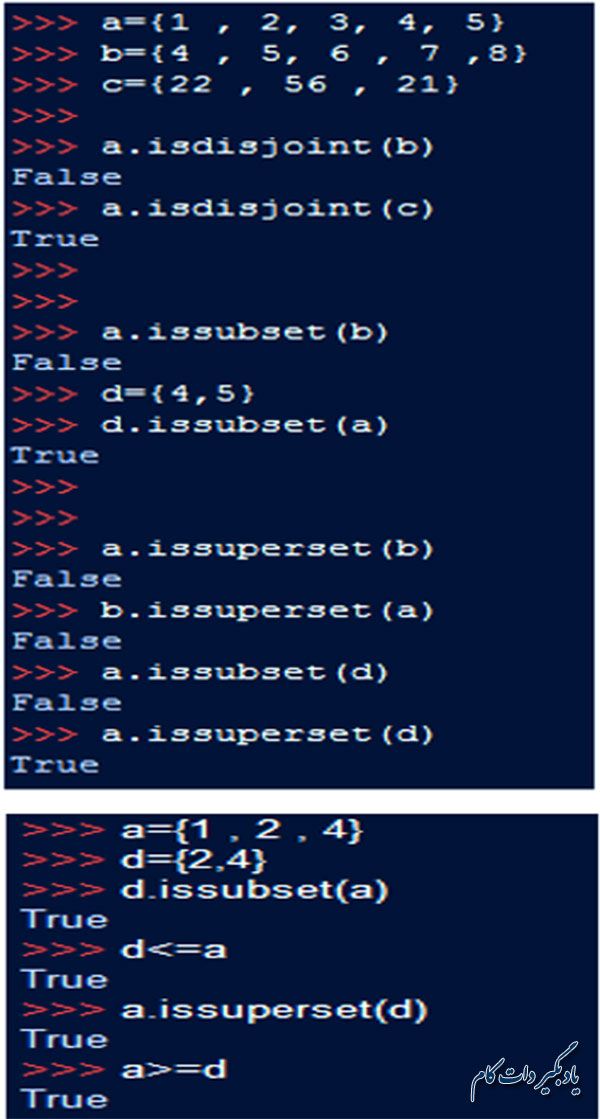
برای بررسی متمایز بودن دو مجموعه هم از تابع isdisjoint() استفاده می کنیم. لذا اگر دو مجموعه هیچ اشتراکی با هم نداشته باشند این تابع مقدارTrue و در غیر این صورت مقدار False را بر می گرداند.
تابع () issubset یا عملگر =>
برای بررسی این که آیا مجموعه اول زیر مجموعه دوم هست یا نه از تابع () issubset استفاده می کنیم. حال اگر مجموعه اول زیر مجموعه، مجموعه دوم باشد این تابع مقدارTrue و در غیر این صورت مقدار False را بر می گرداند.
تابع issuperset() یا عملگر =<
هم چنین برای بررسی این که آیا مجموعه دوم زیرمجموعه مجموعه اول است یا نه از تابع issuperset() استفاده می کنیم. در حقیقت این تابع عکس تابع () issubset عمل می کند. لذا اگر مجموعه اول همه اعضای مجموعه دوم را در خود داشته باشد این تابع مقدارTrue و در غیر این صورت مقدار False را بر می گرداند.
مثلا در قطعه کد زیر می بینید که خروجی دو عبارت d.issubset(a) و a.issuperset(d) با هم یکی هستند.
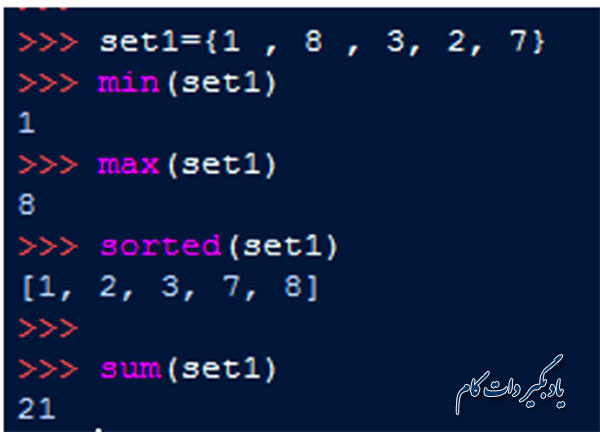
توابع درون ساختهmin() و max() و sum() و sorted()
توابع درون ساخته ای که برای محاسبه کوچک ترین و بزرگ ترین عضو یک مجموعه و نیز مرتب سازی اعضای آن و محاسبه مجموع عناصر یک مجموعه به کار می رود در مثال زیر آورده شده است.
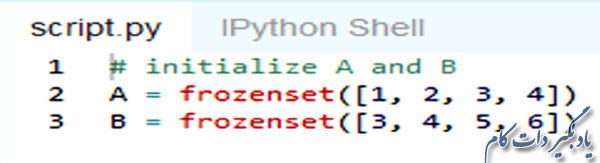
Frozenset های پایتون
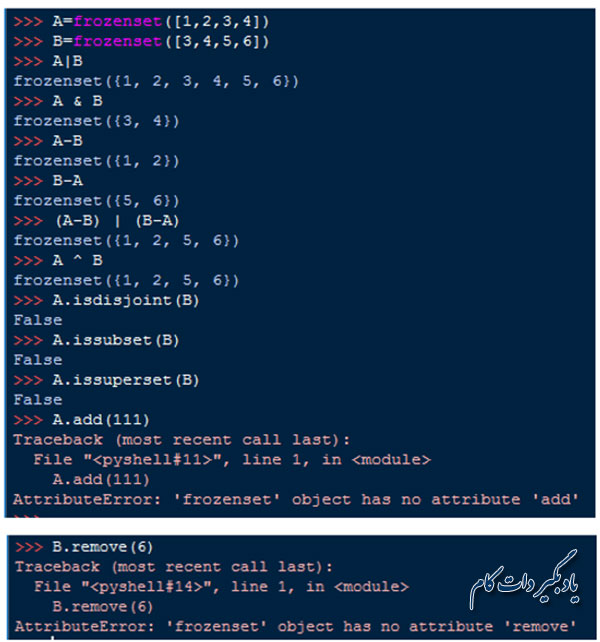
Frozensetکلاس جدیدی است که همه خصوصیات یک مجموعه را دارا می باشد با این تفاوت که عناصر آن نمی توانند تغییر کنند. همان طور که تاپل ها، لیست های تغییرناپذیر هستند، در حقیقت Frozenset ها هم نوعی مجموعه تغییر ناپذیر هستند. Frozenset ها را می توان با تابع Frozenset ایجاد نمود.
این نوع ساختار داده هم مشابه مجموعه ها از توابع زیر پشتیبانی می کند.

ولی به خاطر غیر قابل تغییر بودن ساختمان داده Frozenset ، این نوع داده، فاقد توابع add() و remove() می باشد در نتیجه استفاده از این توابع برای Frozenset ها منجر به خطای AttributeError می شود.
در آموزش زبان پایتون هم چنان با ما همراه باشید.
مقاله بعدی: ساختار های تصمیم گیری پایتون if…else
ترجمه: رقیه آقایاری

















سپاس از این مقاله. خدا قوت عالی بود